The first direct detection of gravitational waves was announced in February of 2015 by the LIGO team, after decades of planning, building and refining their beautiful experiment. Since that time, the US-based LIGO has been joined by the European Virgo gravitational wave telescope (and more are planned around the globe).
The first four events that the teams announced were from the spiralling in and eventual mergers of pairs of black holes, with masses ranging from about seven to about forty times the mass of the sun. These masses are perhaps a bit higher than we expect to by typical, which might raise intriguing questions about how such black holes were formed and evolved, although even comparing the results to the predictions is a hard problem depending on the details of the statistical properties of the detectors and the astrophysical models for the evolution of black holes and the stars from which (we think) they formed.
Last week, the teams announced the detection of a very different kind of event, the collision of two neutron stars, each about 1.4 times the mass of the sun. Neutron stars are one possible end state of the evolution of a star, when its atoms are no longer able to withstand the pressure of the gravity trying to force them together. This was first understood by S Chandrasekhar in the early years of the 20th Century, who realised that there was a limit to the mass of a star held up simply by the quantum-mechanical repulsion of the electrons at the outskirts of the atoms making up the star. When you surpass this mass, known, appropriately enough, as the Chandrasekhar mass, the star will collapse in upon itself, combining the electrons and protons into neutrons and likely releasing a vast amount of energy in the form of a supernova explosion. After the explosion, the remnant is likely to be a dense ball of neutrons, whose properties are actually determined fairly precisely by similar physics to that of the Chandrasekhar limit (discussed for this case by Oppenheimer, Volkoff and Tolman), giving us the magic 1.4 solar mass number.
(Last week also coincidentally would have seen Chandrasekhar’s 107th birthday, and Google chose to illustrate their home page with an animation in his honour for the occasion. I was a graduate student at the University of Chicago, where Chandra, as he was known, spent most of his career. Most of us students were far too intimidated to interact with him, although it was always seen as an auspicious occasion when you spotted him around the halls of the Astronomy and Astrophysics Center.)
This process can therefore make a single 1.4 solar-mass neutron star, and we can imagine that in some rare cases we can end up with two neutron stars orbiting one another. Indeed, the fact that LIGO saw one, but only one, such event during its year-and-a-half run allows the teams to constrain how often that happens, albeit with very large error bars, between 320 and 4740 events per cubic gigaparsec per year; a cubic gigaparsec is about 3 billion light-years on each side, so these are rare events indeed. These results and many other scientific inferences from this single amazing observation are reported in the teams’ overview paper.
A series of other papers discuss those results in more detail, covering the physics of neutron stars to limits on departures from Einstein’s theory of gravity (for more on some of these other topics, see this blog, or this story from the NY Times). As a cosmologist, the most exciting of the results were the use of the event as a “standard siren”, an object whose gravitational wave properties are well-enough understood that we can deduce the distance to the object from the LIGO results alone. Although the idea came from Bernard Schutz in 1986, the term “Standard siren” was coined somewhat later (by Sean Carroll) in analogy to the (heretofore?) more common cosmological standard candles and standard rulers: objects whose intrinsic brightness and distances are known and so whose distances can be measured by observations of their apparent brightness or size, just as you can roughly deduce how far away a light bulb is by how bright it appears, or how far away a familiar object or person is by how big how it looks.
Gravitational wave events are standard sirens because our understanding of relativity is good enough that an observation of the shape of gravitational wave pattern as a function of time can tell us the properties of its source. Knowing that, we also then know the amplitude of that pattern when it was released. Over the time since then, as the gravitational waves have travelled across the Universe toward us, the amplitude has gone down (further objects look dimmer sound quieter); the expansion of the Universe also causes the frequency of the waves to decrease — this is the cosmological redshift that we observe in the spectra of distant objects’ light.
Unlike LIGO’s previous detections of binary-black-hole mergers, this new observation of a binary-neutron-star merger was also seen in photons: first as a gamma-ray burst, and then as a “nova”: a new dot of light in the sky. Indeed, the observation of the afterglow of the merger by teams of literally thousands of astronomers in gamma and x-rays, optical and infrared light, and in the radio, is one of the more amazing pieces of academic teamwork I have seen.
And these observations allowed the teams to identify the host galaxy of the original neutron stars, and to measure the redshift of its light (the lengthening of the light’s wavelength due to the movement of the galaxy away from us). It is most likely a previously unexceptional galaxy called NGC 4993, with a redshift z=0.009, putting it about 40 megaparsecs away, relatively close on cosmological scales.
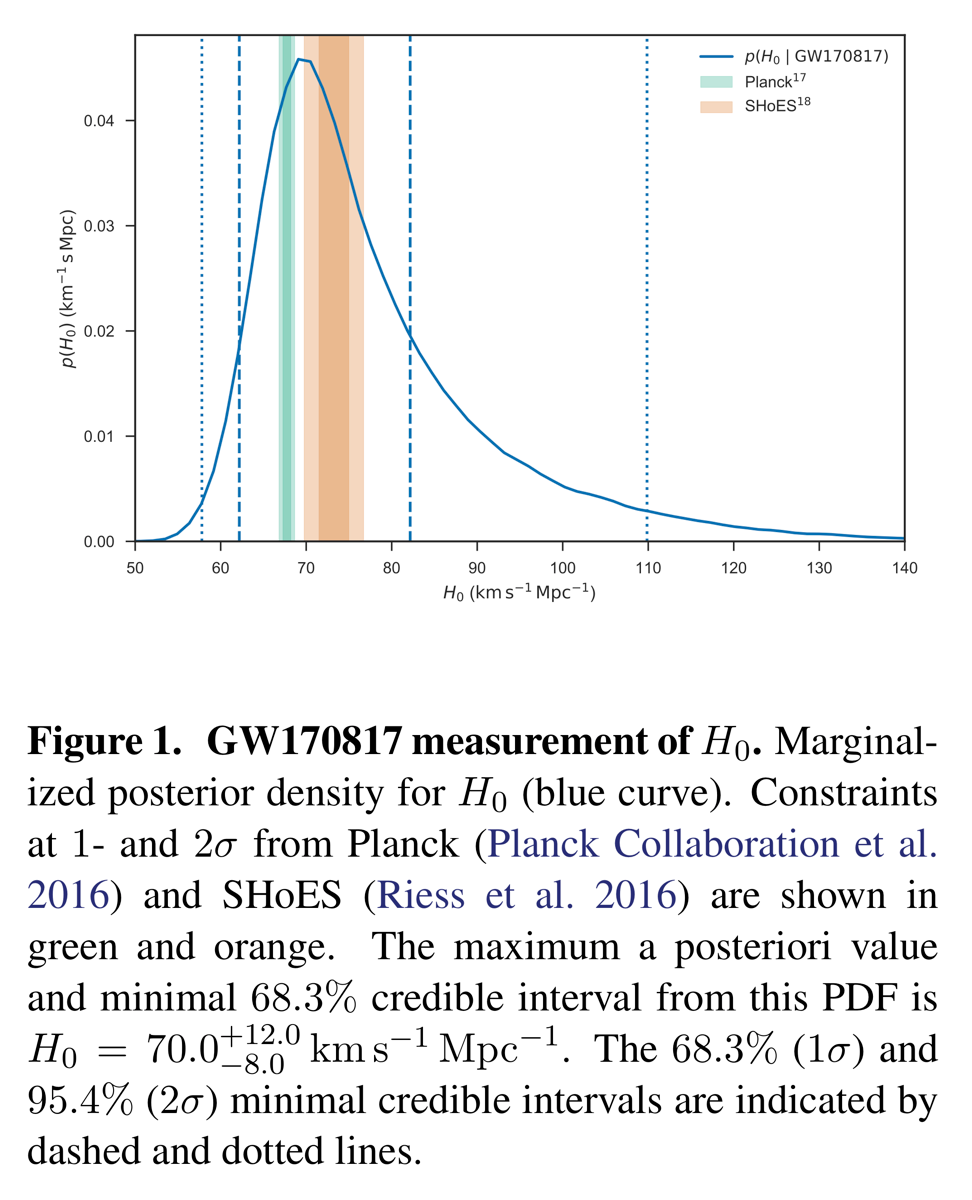
But this means that we can measure all of the factors in one of the most celebrated equations in cosmology, Hubble’s law: cz=H₀ d, where c is the speed of light, z is the redshift just mentioned, and d is the distance measured from the gravitational wave burst itself. This just leaves H₀, the famous Hubble Constant, giving the current rate of expansion of the Universe, usually measured in kilometres per second per megaparsec. The old-fashioned way to measure this quantity is via the so-called cosmic distance ladder, bootstrapping up from nearby objects of known distance to more distant ones whose properties can only be calibrated by comparison with those more nearby. But errors accumulate in this process and we can be susceptible to the weakest rung on the chain (see recent work by some of my colleagues trying to formalise this process). Alternately, we can use data from cosmic microwave background (CMB) experiments like the Planck Satellite (see here for lots of discussion on this blog); the typical size of the CMB pattern on the sky is something very like a standard ruler. Unfortunately, it, too, needs to calibrated, implicitly by other aspects of the CMB pattern itself, and so ends up being a somewhat indirect measurement. Currently, the best cosmic-distance-ladder measurement gives something like 73.24 ± 1.74 km/sec/Mpc whereas Planck gives 67.81 ± 0.92 km/sec/Mpc; these numbers disagree by “a few sigma”, enough that it is hard to explain as simply a statistical fluctuation.
Unfortunately, the new LIGO results do not solve the problem. Because we cannot observe the inclination of the neutron-star binary (i.e., the orientation of its orbit), this blows up the error on the distance to the object, due to the Bayesian marginalisation over this unknown parameter (just as the Planck measurement requires marginalization over all of the other cosmological parameters to fully calibrate the results). Because the host galaxy is relatively nearby, the teams must also account for the fact that the redshift includes the effect not only of the cosmological expansion but also the movement of galaxies with respect to one another due to the pull of gravity on relatively large scales; this so-called peculiar velocity has to be modelled which adds further to the errors.
This procedure gives a final measurement of 70.0+12-8.0, with the full shape of the probability curve shown in the Figure, taken directly from the paper. Both the Planck and distance-ladder results are consistent with these rather large error bars. But this is calculated from a single object; as more of these events are seen these error bars will go down, typically by something like the square root of the number of events, so it might not be too long before this is the best way to measure the Hubble Constant.
[Apologies: too long, too technical, and written late at night while trying to get my wonderful not-quite-three-week-old daughter to sleep through the night.]