Yesterday, we at Imperial hosted the latest instalment of the London Cosmology Discussion Meetings (LCDM, which is a cosmology in-joke, of course), with about 40 participants — most of them students — from Imperial, QMUL and UCL. We heard talks about observing clusters of galaxies, different theories of gravity, and the observational repercussions of cosmic inflation. One excellent talk by UCL’s Chris Sabiu, drew my attention to an amazing 1941 paper by Erik Holmberg, “On the Clustering Tendencies among the Nebulae. II. a Study of Encounters Between Laboratory Models of Stellar Systems by a New Integration Procedure.”
This paper is one of the earliest attempts at a gravitational n-body simulation, calculating the motion of a pair of very simplified galaxies, each with only 37 “stars”. But Holmberg realized that to calculate the net force on any one of the stars requires knowing the force from each of the 73 other stars, and that he had to do this for each of the stars, therefore scaling overall like the square of the total number (more than 5000 pairs, taking symmetry into account), and that he would have to do this whole calculation at each step of time. This would be too much work with the pencil and paper available at the time for doing computations (the first digital computer simulations weren’t done until the early 1960s).
The important words in the title are “Laboratory Models” — Instead of calculation, Holmberg found an analogy with another physical system: light, whose intensity obeys an inverse-square law just like the gravitational force. Moreover, both the intensity and the gravitational force add up (we say “superpose” in physics). So by replacing his gravitating stars with shining light bulbs, and putting a light-meter at the location of each one, he could replace the 5000 calculations with 74 meter-readings.
With this setup, Holmberg was able to do genuinely new science, understanding the impact of tidal forces on galaxy interactions (tidal forces vary across a single object and the difference causes it to stretch, just as the tides raised by the Moon distort the shape of the Earth’s oceans).
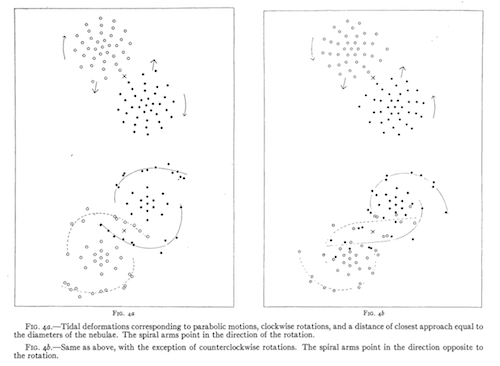
This is a wonderful example of an “analog computer”, and just a brilliant concept, taking something that everyone who has ever studied physics has noticed — the similarity between gravitational force and intensity — and putting it to work. Current n-body simulation codes have managed to improve upon the naive expectation of scaling like the square of the number of particles in the simulation, but actually not quite as well as Holmberg’s version which scales linearly with the number, since he lets light’s properties do much of the work for him. I don’t know many scientists who have had such a creative idea in their whole careers.